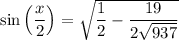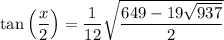If x is in quadrant I, then both sin(x) and cos(x) are positive. The angle x/2 also belongs to quadrant I, and hence each of sin(x/2), cos(x/2), and tan(x/2) are positive.
Recall that for all x,
cos²(x) + sin²(x) = 1
and multiplying through both sides by 1/cos²(x) = sec²(x) gives another flavor of this identity,
1 + tan²(x) = sec²(x)
It follows that
sec(x) = √(1 + tan²(x)) = √937/19
which immediately gives us
cos(x) = 19/√937
and from the identity above we find
sin(x) = √(1 - cos²(x)) = 24/√937
Recall the half angle identity for cos :
cos²(x) = (1 + cos(2x))/2
which means
cos(x/2) = + √[(1 + cos(x))/2] = √[1/2 + 19/(2√937)]
Then
sin(x/2) = + √(1 - cos²(x/2)) = √[1/2 - 19/(2 √937)]
and by definition of tan,
tan(x/2) = sin(x/2) / cos(x/2) = 1/12 √[649/2 - 19 √937/2]
Just to be clear, the solutions are