Answer:
Confidence level is (380.7133, 533.2867)
Explanation:
Responses in number of tongue flicks per 20 minutes of lizards, are: 727,217, 268, 438, 625, 319, 200, 591, 574, 727, 693, 336, 302, 761, 268, 353, 370
n = 17
Mean (μ) is:
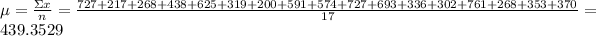
Standard deviation (σ) is:
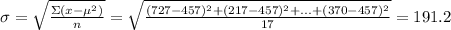
The confidence interval (c) = 90% = 0.9
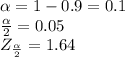
Margin of error (e) =
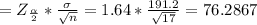
Confidence level = μ ± e = 457 ± 76.2867 = (380.7133, 533.2867)