Question

In a clinical trial for a new drug 15 men and 21 women volunteered. Needing a representative sample from both sexes, how many selection options are available if 11 men and 17 women are to be selected for the trial?

Answer 1

• 8,169,525

Step-by-step explanation:

Following the fundamental counting principle, the number of selection options is the product of the number of the different selection options for the 11 men by the number of different selection options for 17 women.

1. Number of different selection options for 11 men

Since the order does not matter (i.e. for 11 given men it is the sae any order in which they are selected), the number of different selections is given by the formula of combinations:

`C(m,n)=(m!)/(n!(m-n)!)`

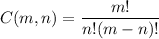
You want to select 11 men from a sample of 15 men, then:

`C(15,11)=(15!)/(11!(15-11)!)=1,365`

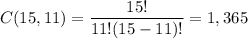
2. Number of different selection option for 17 women

Following the same reasoning, to select 17 women from the sample os 21 women:

`C(21,17)=(21!)/(17!(21-17)!)=5,985`

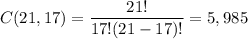
3. Number of different selection options available if 11 men and 17 women are to be selected bor the trial:

As explained above, compute the product: C(15,11) × (C21,17):

• 1,365 × 5,985 = 8,169,525 ← answer