Answer:
Magnetic force,

Step-by-step explanation:
Given that,
A beryllium-9 ion has a positive charge that is double the charge of a proton,
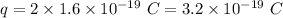
Speed of the ion in the magnetic field,
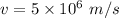
Its velocity makes an angle of 61° with the direction of the magnetic field at the ion's location.
The magnitude of the field is 0.220 T.
We need to find the magnitude of the magnetic force on the ion. It is given by :
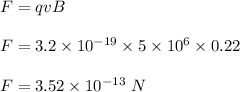
So, the magnitude of magnetic force on the ion is
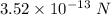 .
.