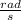Answer:
The angular speed of the record is 1.8
Step-by-step explanation:
Given:
Mass
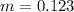 kg
kg
Radius
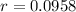 m
m
Angular speed
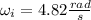
Moment of inertia
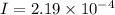
Mass of putty
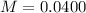 Kg
Kg
For finding the final angular speed,
According to the conservation of angular momentum,
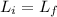
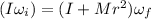
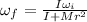

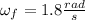
Therefore, the angular speed of the record is 1.8