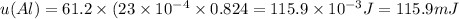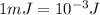Answer with Explanation:
We are given that
Length of solenoid,l=82.4 cm=

1m=100 cm
Area,A=
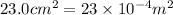
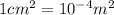
Number of turns,N=1380
Current,I=5.89 A
a.Magnetic field of solenoid,
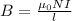
Where
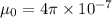
Using the formula
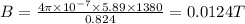
Energy density of the magnetic field inside the solenoid=

b.Total energy stored in the magnetic field=