Question

Winner’s curse ~ In auction bidding, the "winner’s curse" is the phenomenon of the winning bid price being above the expected value of the item being auctioned. In a study, two groups of bidders were compared in a sealed-bid auction, super-experienced bidders and less-experienced bidders. In the super-experienced group, 28 of 189 winning bids were above the item’s expected value. In the less-experienced group, 33 of 149 winning bids were above the item’s expected value. We want to determine if the proportion of winning bids that were above the item’s expected value for the super-experienced bidders is less than that in the less-experienced bidders. Notation: 1=super-experienced bidders and 2=less-experienced bidders. What are the null and alternative hypothesis for this hypothesis test? Question 12 options: Null hypothesis Alternative hypothesis 1. p1=p2 2. pˆ1=pˆ2 3. p1≠p2 4. pˆ1≠pˆ2 5. p1>p2 6. pˆ1>pˆ2 7. p1

Answer 1

At a significance of 0.05, the null hypothesis failed to be rejected.

There is no enough evidence to claim that the proportion of winning bids that were above the item’s expected value for the super-experienced bidders is less than that in the less-experienced bidders, although the P-value is really close to the significance level (P-value=0.052).

Explanation:

We have to perform an hypothesis test on the difference of proportions.

The null and alternative hypothesis are:

`H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2<0`

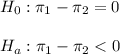
The significance level is assumed to be α=0.05.

The difference in sample proportions is:

`p_1=28/189=0.15\\\\p_2=33/149=0.22\\\\\\p_1-p_2=0.15-0.22=-0.07`

The standard error for the difference of proportions is:

`\sigma_(p_1-p_2)=\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2)}\\\\ \sigma_(p_1-p_2)=\sqrt{(0.15*0.85)/(189)+(0.22*0.78)/(149)}\\\\ \sigma_(p_1-p_2)=√( 0.000674603+0.001151678)\\\\ \sigma_(p_1-p_2)=√(0.001826281)\\\\ \sigma_(p_1-p_2)=0.043`

The test statistic can be calculated as:

`z=(p_1-p_2)/(\sigma_p)=(-0.07)/(0.043) =-1.63`

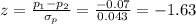
The P-value for this test statistic is:

`P-value=P(z<-1.67)=0.052`

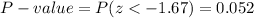
The P-value is bigger than the significance level.

At a significance of 0.05, the null hypothesis failed to be rejected.

There is no enough evidence to claim that the proportion of winning bids that were above the item’s expected value for the super-experienced bidders is less than that in the less-experienced bidders, although the P-value is really close to the significance level.