Answer:
0.9146 = 91.46% probability that the proportion of persons with a college degree will differ from the population proportion by less than 4%
Explanation:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
For the sampling distribution of a sample proportion of size n, we have that
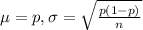
In this problem, we have that:
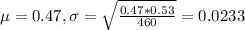
What is the probability that the proportion of persons with a college degree will differ from the population proportion by less than 4%?
Population proportion between 0.47-0.04 = 0.43 and 0.47+0.04 = 0.51, which is the pvalue of Z when X = 0.51 subtracted by the pvalue of Z when X = 0.43. So
X = 0.51

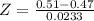

 has a pvalue of 0.9573
has a pvalue of 0.9573
X = 0.43

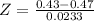

 has a pvalue of 0.0427
has a pvalue of 0.0427
0.9573 - 0.0427 = 0.9146
0.9146 = 91.46% probability that the proportion of persons with a college degree will differ from the population proportion by less than 4%