Question

Humans evolved in Earth's atmosphere, therefore the pressures interior to the body are relatively close to atmospheric pressure. Because the differences between internal body pressures and atmospheric pressure are so small, individuals have a difficult time gauging the magnitude of atmospheric pressure. Suppose an individual is lying on his stomach with sheets of paper stacked on his back. If each sheet of paper has a mass of 0.00320 kg and is the standard letter size of 8.5 in by 11 in ( 0.216 m by 0.279 m ), how many sheets must be stacked to produce a pressure on his back equal to atmospheric pressure (roughly 101325 Pa )?

Answer 1

193664 sheets of paper.

Step-by-step explanation:

We know that the pressure is defined as

`p=(F)/(A)`

In words, the applied force divided by the area of application. The area of a single sheet of paper is

`A=bh\\\\A=(0.216m)(0.279m)=0.060m^(2)`

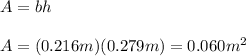
The force exerted by a single sheet of paper is its weight, given by teh expression:

`F=mg`

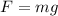
(Where m is the mass of a single sheet and g is the acceleration due to gravity on earth)

And, for
`n` sheets of paper, the total weight is:

`F=nmg`

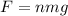
Now, substituting this in the definition of pressure and solving for
`n`, we get:

`p=(nmg)/(A)\\\\ \implies n=(pA)/(mg)`

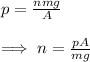
Finally, plugging in the known values, we can compute
`n`:

`n=((101325Pa)(0.060m^(2) ))/((0.00320kg)(9.81m/s^(2)))\\\\n=193664`

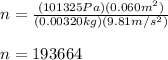
This means that there must be 193664 sheets stacked to produce a pressure equal to atmospheric pressure.

Answer 2

194516 sheets

Step-by-step explanation:

So the area of each sheet of paper is:

A = 0.216 * 0.279 = 0.060264 square meters

For the paper sheet to make the same effect as the atmospheric pressure P, then the gravity F from the paper sheet must be

F = AP = 0.060264 * 101325 = 6106 N

Let g = 9.81 m/s2, then the mass of paper needed to generate that gravity is

m = F/g = 6106 / 9.81 = 622.4 kg

If each sheet has a mass of 0.0032 kg, then the total number of sheets to have that much mass is

622.4 / 0.0032 = 194516 sheets