Question

A conducting spherical shell with inner radius a and outer radius b has a positive point charge +Q at the center in the empty region. The excess charge on the conducting shell is -3Q. (a) What are the charges on the inner and outer surface of the shell? [2] (b)Derive the expression for E field as a function of distance r and Q for r b. [1.5] (c) Sketch E as a function of r from the center outward. [1] (d) How would the answers to part (a) and (b) (part (b) only for ab) change if the charge Q was not at the center inside the shell but away from it but still in the empty region? [1.5]

Answer 1

a) q_inner = -Q

, q_outer = -2Q

b) E₁ = k Q / r² r<a

E₂ = 0 a<r<b

E₃ = - k 2Q/r² r>b

d) the charge continues inside the spherical shell, the results do not change

Step-by-step explanation:

a) The point load in the center induces a load on the inner surface of the shell with constant opposite sign

q_inner = -Q

the outer shell of the shell the load is

q_outer = -3 Q + Q

q_outer = -2Q

b) To find the electric field again, use Gauss's law,

We define as a Gaussian surface a sphere

Ф = E. dA =
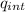`q_(int)`/ε₀

in this case the electric field lines and the radii of the sphere are parallel, so the sclar product is reduced to the algegraic product

E A = q_{int}/ε₀

the area of ​​a sphere is

A = 4 π r²

E = 1 / 4πε₀ Q/ r²

k = 1 / 4πε₀

let's apply this expression to the different radii

i) r <a

in this case the load inside is the point load

`q_(int)`= + Q

E₁ = k Q / r²

ii) the field inside the shell

a <r <b

As the sphere is conductive, so that it is in electrostatic equilibrium, there can be no field within it.

E₂ = 0

iii) r>b

q_{int} = Q- 3Q = -2Q

E₃ = k (-2Q/r²)

E₃ = - k 2Q/r²

c) see attached

d) as the charge continues inside the spherical shell, the results do not change, since the lcharge inside remains the same and it does not matter its precise location, but remains within the Gaussian surface