Question

The mass of block A is 4 kg, the mass of block B is 3 kg, and the angle of the ramp is θ = 30°. The rope moves over the pulley without slipping. The coefficient of kinetic friction between the block A and the ramp is 0.15. The pulley can be modeled as a uniformly dense cylinder with a mass of 4 kg and a radius of 10 cm. What is the magnitude of the tension (in N) in the rope between block B and the pulley?

Answer 1

`T_(B)=26.16 N`

Step-by-step explanation:

We need to use the Newton's second law.

Block A

`\Sigma F=m_(A)a`

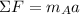
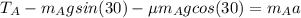`T_(A)-m_(A)gsin(30)-\mu m_(A)gcos(30)=m_(A)a` (1)

Block B

`\Sigma F=m_(B)a`

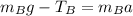`m_(B)g-T_(B)=m_(B)a` (2)

Pulley

Here we need to use Newton's law related to the torque.

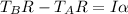`T_(B)R-T_(A)R=I\alpha` (3)

I is the momentum of inertia of a cylinder (I=(1/2)mr²)

α is the angular acceleration (a/R)

Let's combine 1 and 2 to find T(B)-T(A)

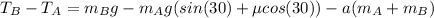`T_(B)-T_(A)=m_(B)g-m_(A)g(sin(30)+\mu cos(30))-a(m_(A)+m_(B))` (4)

From 3 we have:

`T_(B)R-T_(A)R=(1/2)m_(p)R^(2)*(a/R)`

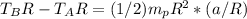
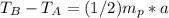`T_(B)-T_(A)=(1/2)m_(p)*a` (5)

We can equal (4) and (5)

`(1/2)m_(p)*a=m_(B)g-m_(A)g(sin(30)+\mu cos(30))-a(m_(A)+m_(B))`

`(1/2)m_(p)*a+a(m_(A)+m_(B))=m_(B)g-m_(A)g(sin(30)+\mu cos(30))`

`a((1/2)m_(p)+(m_(A)+m_(B)))=m_(B)g-m_(A)g(sin(30)+\mu cos(30))`

`a=(m_(B)g-m_(A)g(sin(30)+\mu cos(30)))/((1/2)m_(p)+(m_(A)+m_(B)))`

`a=(3*9.81-4*9.81*(sin(30)+0.15cos(30)))/((1/2)*4+(4+3))`

`a=0.52 m/s^(2)`

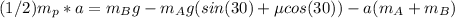
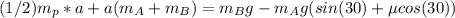
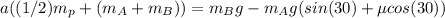
Therefore, using (2) we can find the tension in the rope between block B:

`T_(B)=m_(B)g-m_(B)a`

`T_(B)=m_(B)(g-a)`

`T_(B)=27.87 N`

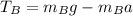
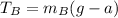
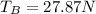
I hope it helps you!