Answer:
Expected duration between when orders begin and production begins = 12.55 days
Explanation:
Expected duration between when an order is received and the start of production:
Average production time for a bag, P = 1.8
Standard deviation,
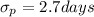
Number of employees, m = 2
Larry expects one customer order a day, a = 1
Coefficient of variation of arrival,
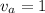
Coefficient of variation of processing,
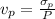
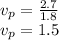
Utilization,
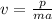


Expected time of wait =
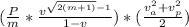
Expected time of wait =
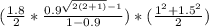
Expected time of wait = 12.55 days