Answer:
The sample size is 74
Pbar = 0.05
The variance information is needed
Explanation:
The population variance ,
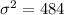
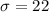
Confidence Interval level = 95% = 0.95
Significance Interval = 1 - CI
Significance Interval = 1 - 0.95 = 0.05
Error margin = 5
The critical value =
 = 1.96 (From the z table)
= 1.96 (From the z table)
The sample size is given by:
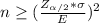
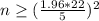
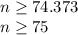
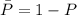
Since P = 0.95
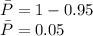
The variance information is needed in this question when calculating the sample size