Question

In two-photon ionization spectroscopy, the combined energy of two different photons is used to remove an electron from an atom or molecule. In such an experiment, a potassium atom in the gas phase is ionized by two different lasers, one of which has a wavelength of 770.0 nm. What is the maximum wavelength for the second laser that will cause two-photon ionization? The ionization energy of potassium is 6.96E-19 J. nm

Answer 1

To induce two-photon ionization in potassium with an ionization energy of 4.34 eV using one laser at 770.0 nm, the maximum wavelength of the second laser must be approximately 454.54 nm.

Step-by-step explanation:

The student asks about the maximum wavelength of the second laser that can cause two-photon ionization in a potassium atom when one laser with a wavelength of 770.0 nm is already being used. The ionization energy of potassium is given as 6.96E-19 J.

To solve this, we first convert the ionization energy from joules to electron volts (eV), using the conversion factor of 1 eV = 1.602 x 10-19 J:

Ionization energy (eV) =
`6.96E-19 J / (1.602 x 10-19 J/eV) = 4.34 eV`

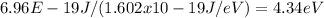
The energy of the first photon is calculated by using the energy-wavelength relation E = hc/λ, where h is Planck's constant, c is the speed of light, and λ is the wavelength.

Energy of the first photon (eV) =
`(4.1357 x 10-15 eV*s)(3 x 108 m/s) / 770 x 10-9 m`

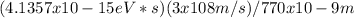
Energy of the first photon (eV) = 1.61 eV

Since two photons are used for ionization, we need to find the energy of the second photon. The combined energy of the two photons must be equal to or greater than the ionization energy:

Energy of the second photon (eV) = Ionization energy - Energy of the first photon

Energy of the second photon (eV) = 4.34 eV - 1.61 eV

Energy of the second photon (eV) = 2.73 eV

Now, we can calculate the maximum wavelength of the second photon using the same energy-wavelength relation:

λmax = hc / Energy of the second photon

λmax =
`(4.1357 x 10-15 eV*s)(3 x 108 m/s) / 2.73 eV`

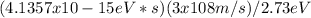
λmax = 454.54 nm

Therefore, the maximum wavelength for the second laser that will cause two-photon ionization of potassium is approximately 454.54 nm.

Answer 2

The maximum wavelength of second laser is 453.8 nm

Step-by-step explanation:

Given:

Wavelength of light
`\lambda = 770 * 10^(-9)` m

Ionization energy of potassium
`= 6.96 * 10^(-19)` J

First find the energy related to the one of light,

`E = (hc)/(\lambda)`

Where
`h = 6.626 * 10^(-34)`,
`c = 3 * 10^(8) (m)/(s)`

`E = (6.626 * 10^(-34) * 3 * 10^(8) )/(770 * 10^(-9) )`

`E = 2.58 * 10^(-19)`J

This is the energy of the first laser, the missing energy is given by.

`E' = (6.96 - 2.58) * 10^(-19)`

`E ' = 4.38 * 10^(-19)`J

For finding wavelength of second laser,

`E' = (hc)/(\lambda ')`

`\lambda ' = (hc)/(E')`

`\lambda ' = (6.626 * 10^(-34) * 3 * 10^(8) )/(4.38 * 10^(-19) )`

`\lambda ' = 453.8 * 10^(-9 )` m

`\lambda ' = 453.8` nm

Therefore, the maximum wavelength of second laser is 453.8 nm