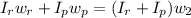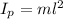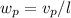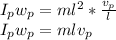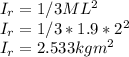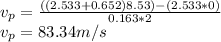Question

If the rod makes one revolution every 0.736 s after the puck is caught, what was the puck's speed just before it hit the rod? (See details).A local ice hockey team has asked you to design an apparatus for measuring the speed of the hockey puck after a slap shot. Your design is a 2.00-m-long, uniform rod pivoted about one end so that it is free to rotate horizontally on the ice without friction. The 1.90-kg rod has a light basket at the other end to catch the 0.163-kg puck. The puck slides across the ice with velocity v (perpendicular to the rod), hits the basket, and is caught. After the collision, the rod rotates.

Answer 1

Pluck velocity = 83.34 m/s

Step-by-step explanation:

The initial angular speed of the rod before it was hit,
`w_(r) = 0`

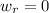
The angular speed of the rod and pluck rotating together,
`w_(2) = (2\pi )/(T)`

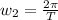
The period of rotation, T = 0.736 s

`w_(2) = (2\pi )/(0.736)\\w_(2) = 8.53 rad/s`

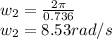
Using the principle of conservation of angular momentum:

`I_(r) w_(r) + I_(p) w_(p) = (I_(r)+ I_(p)) w_(2)`

`I_(p) = ml^(2)`

`w_(p) = v_(p) /l`

`I_(p) w_(p) = ml^(2) * (v_(p) )/(l) \\I_(p) w_(p) = mlv_(p)`

`I_(r) w_(r) +mlv_(p) = (I_(r)+ I_(p)) w_(2)\\mlv_(p) =( (I_(r)+ I_(p)) w_(2) ) - I_(r) w_(r)\\v_(p) = (( (I_(r)+ I_(p)) w_(2) ) - I_(r) w_(r))/(ml)`

`I_(r) = 1/3 ML^(2) \\I_(r) = 1/3 * 1.9 * 2^(2) \\I_(r) = 2.533 kg m^(2)`

`I_(p) = ml^(2) \\I_(p) = 0.163 * 2^(2) \\I_(p) = 0.652 kgm^(2)`

`v_(p) = (( (2.533+0.652) 8.53 ) - (2.533* 0))/(0.163*2)\\v_(p) = 83.34 m/s`