Given:
Given that there are 4 expressions.
We need to determine the expressions that are polynomials.
Option a:
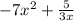
In the second term of the expression, the constant is divided by a variable.
For an expression to be a polynomial, it should not divided by a variable.
Hence, the expression
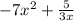 is not a polynomial.
is not a polynomial.
Thus, Option a is not the correct answer.
Option b:
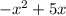
The given expression satisfies the conditions of the polynomial.
Hence, the expression
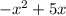 is a polynomial.
is a polynomial.
Thus, Option b is the correct answer.
Option c:
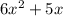
The given expression satisfies the conditions of the polynomial.
Hence, the expression
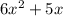 is a polynomial.
is a polynomial.
Thus, Option c is the correct answer.
Option d:
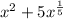
The second term of the expression contains the exponent
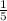
For an expression to be a polynomial, the fractional exponent is not allowed.
Hence, the given expression
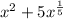 is not a polynomial.
is not a polynomial.
Thus, Option d is not the correct answer.