Question

Find the GCF of the following monomials.

-50m4n7 and 40m2n10

Answer 1

Assuming you are asking for the Greatest Common Factor (GCF) of
`-50m^4n^7` and
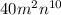`40m^2n^(10)` the answer is:

`10m^2n^7`

Explanation:

To find the GCF we should first find the GCF of the coefficients 50 and 40 which is 10.

After factoring that out we need to take a look at the variable m. In monomial 1 we see that the highest exponent of m is 4 and in the second is 2. When finding GCF we take the smallest of the two exponents which is 2. Therefore the next part of our GCF monomial is m²

If we apply the same rule for n the smallest exponent is 7 resulting in the appending of
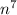`n^(7)` to the answer

After combining each of these GCF of 40 and -50 (10), m^4 and m² (m²), and n^7 and n^10 (n^7) the answer is:

`10m^2n^7`