Question

In a live fire exercise, an Army artillery team fires an artillery shell from a howitzer. The barrel of the howitzer makes a 50.0° angle above horizontal, and the speed of the shell upon exiting the barrel is 360 m/s. The shell hits a target on the side of a mountain 38.0 s after firing. Assuming the point where the shell exits the barrel to be the origin, and assuming as usual that the x-axis is horizontal and the y-axis is vertical, find the x and y coordinates, in meters, of the target.

Answer 1

The coordinates of the target are (8790m, 3400m).

Step-by-step explanation:

First of all, we have to find the components of the initial velocity
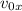`v_0_x` and
`v_0_y`, using trigonometry:

`v_0_x=v_0\cos\theta=(360m/s)\cos50\°=231.4m/s\\\\v_0_y=v_0\sin\theta=(360m/s)\sin50\°=275.7m/s`

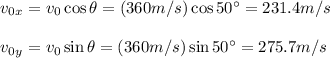
Now, we find the x-coordinate using the equation of motion with constant speed (since there is no external force in x-axis that causes an horizontal acceleration):

`x=v_0_xt\\\\x=(231m/s)(38.0s)=8790m`

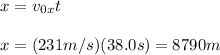
Then, we find the y-coordinate using the equation of position of an object with constant acceleration (since there is the gravitational force causing a vertical acceleration on the shell):

`y=v_0_yt-(1)/(2)gt^(2)\\\\y=(276m/s)(38.0s)-(1)/(2)(9.81m/s^(2))(38.0s)^(2)=3400m`

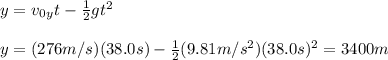
Finally, the coordinates of the target are (8790m, 3400m).