We are given the equation x² + 8x = 33, and we need to solve it from completing the square, for which we will be following the below steps
Step 1 :- First, notice, what's the coefficient of x², if it's 1, then proceed to step 2, if not then divide both sides by the coefficient of x²
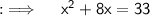
Step 2 :- Here, we need to develop a whole square in both sides somehow, so we have the coefficient of x, so add the square of half of coefficient of x on both sides :
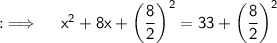
Simplify both sides now :
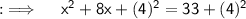
Step 3 :- So now, here LHS is in the form of a² + 2ab + b², so we can just replace it by (a + b)², and we will keep simplifying RHS
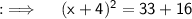
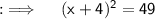
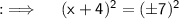
Step 4 :- As, power on both sides is 2, so we can just equate the bases
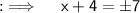
Step 5 :- Equating x + 4 to 7, will yield x = 3, and equating it to -7, will yield x = -11, so we are now left with
