Question

Health insurers are beginning to offer telemedicine services online that replace the common office visit. Wellpoint provides a video service that allows subscribers to connect with a physician online and receive prescribed treatments. Wellpoint claims that users of its LiveHealth Online service saved a significant amount of money on a typical visit.

The data shown below ($), for a sample of 20 online doctor visits, are consistent with the savings per visit reported by Wellpoint.

92 34 40
105 83 55
56 49 40
76 48 96
93 74 73
78 93 100
53 82

Assuming the population is roughly symmetric, construct a 95% confidence interval for the mean savings for a televisit to the doctor as opposed to an office visit.

Answer 1

The 95% confidence interval for the mean savings is ($60.54, $81.46).

Explanation:

As there is no information about the population standard deviation of savings and the sample is not large, i.e. n = 20 < 30, we will use a t-confidence interval.

The (1 - α)% confidence interval for population mean (μ) is:

`CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))`

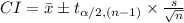
For the data provided compute the sample mean and standard deviation as follows:

`\bar x=(1)/(n)\sum\limits^(n)_(i=1){ X_(i)}=(1)/(20)* [92+34+40+...+53+82]=71`

`s= \sqrt{ \frac{ \sum{\left(x_i - \overline{X}\right)^2 }}{n-1} } = \sqrt{ ( 9492 )/( 20 - 1) } \approx 22.35`

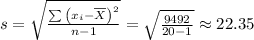
The critical value of t for α = 0.05 and (n - 1) = 19 degrees of freedom is:

`t_(\alpha/2, (n-1))=t_(0.025, 19)=2.093`

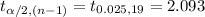
*Use a t-table for the value.

Compute the 95% confidence interval for the mean savings as follows:

`CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))\\=71\pm 2.093*(22.35)/(√(20))\\=71\pm 10.46\\=(60.54, 81.46)`

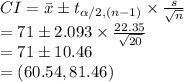
Thus, the 95% confidence interval for the mean savings is ($60.54, $81.46).