Question

In order to determine the average weight of carry-on luggage by passengers in airplanes, a sample of 36 pieces of carry-on luggage was weighed. The average weight was 20 pounds. Assume that we know the standard deviation of the population to be 8 pounds.

assume for part be that we do not kow the standard deviation. a determine a 95% confidence interval estimate for the mean weight fo the carry-on luggage. b determine the 97% confidence interval

Answer 1

a) The 95% confidence interval estimate for the mean weight fo the carry-on luggage

(17.38 , 22.61)

b) The 97% confidence interval estimate for the mean weight of the carry-on luggage

(17.11 , 22.89)

Explanation:

Step1:-

a sample of 36 pieces of carry-on luggage was weighed

n=36

The average weight was 20 pounds

x⁻ = 20

given standard deviation of the population to be 8 pounds.

σ = 8

Confidence intervals :-

The values
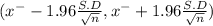`(x^(-) - 1.96 (S.D)/(√(n) ) ,x^(-) + 1.96 (S.D)/(√(n) ) )` are called 95% of Confidence intervals for the mean of the population corresponding to the given sample.

The values
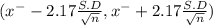`(x^(-) - 2.17 (S.D)/(√(n) ) ,x^(-) + 2.17 (S.D)/(√(n) ) )` are called 97% of Confidence intervals for the mean of the population corresponding to the given sample.

Step:-(1)

The 95% confidence interval estimate for the mean weight of the carry-on luggage

`(x^(-) - 1.96 (S.D)/(√(n) ) ,x^(-) + 1.96 (S.D)/(√(n) ) )`

`(20 - 1.96 (8)/(√(36) ) ,20 + 1.96 (8)/(√(36) ) )`

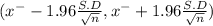
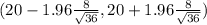
on calculation , we get

(20 -2.613 ,20 +2.613)

(17.3866 , 22.613)

The 95% confidence interval estimate for the mean weight fo the carry-on luggage

(17.3866 , 22.613)

Step2:-

The 97% confidence interval estimate for the mean weight of the carry-on luggage

`(x^(-) - 2.17 (S.D)/(√(n) ) ,x^(-) + 2.17 (S.D)/(√(n) )`

`(20 - 2.17 (8)/(√(36) ) ,20 + 2.17 (8)/(√(36) ) )`

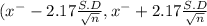
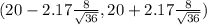
on calculation , we get

(20-2.89 , 20+2.89)

(17.11 , 22.89)

The 97% confidence interval estimate for the mean weight of the carry-on luggage

(17.11 , 22.89)