Question

In a double-slit experiment, the slits are illuminated by a monochromatic, coherent light source having a wavelength of 507 nm. An interference pattern is observed on the screen. The distance between the screen and the double-slit is 1.32 m and the distance between the two slits is 0.112 mm. A light wave propogates from each slit to the screen. What is the path length difference between the distance traveled by the waves for the fifth-order maximum (bright fringe) on the screen

Answer 1

The path difference is
`2.53 * 10^(-6)` m

Step-by-step explanation:

Given:

Wavelength of light
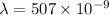`\lambda = 507 * 10^(-9)` m

Distance between slit and screen
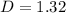`D = 1.32` m

Distance between two slit
`d = 0.112 * 10^(-3)` m

Order of interference
`n = 5`

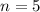
From the formula of interference of light,

`d\sin \theta = n\lambda`

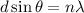
Where
`d \sin \theta =` path difference,
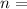`n =` order of interference

Here we have to find path difference,

Path difference
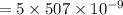`= 5 * 507 * 10^(-9)` m

Path difference
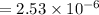`= 2.53 * 10^(-6)` m

Therefore, the path difference is
`2.53 * 10^(-6)` m