Question

The base radius of a cone is expanding at the rate of 1in/min while its height is shrinking at the rate of 3in/min. How fast is the volume of this cone changing at the moment when the base radius is 30 in and the height is 40in?

Answer 1

The volume of the cone is shrinking at the rate
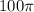`100\pi` cubic inches / min.

Explanation:

Formula:

• 
  `(d)/(dx)(uv)=v(du)/(dt)+u(dv)/(dt)`
• 
  `(d)/(dx)(u^n)=nu^(n-1)(du)/(dx)`

Given that,

The base of a cone is expanding at the rate of 1 in / min while it height is shrinking at the rate 3 in/ min.

i.e

`(dr)/(dt)=1 \ in/min`

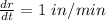
and

`(dh)/(dt)= -3 \ in/min` [ since height is shirking]

The volume of a cone is

`V=\frac13 \pi r^2h`

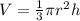
Differentiating with respect to t

`(dV)/(dt) =\frac13\pi \{h (d)/(dt)(r^2)+r^2(d)/(dt)(h)\}`

`\Rightarrow(dV)/(dt)=\frac13\pi (h.2r (dr)/(dt)+r^2(dh)/(dt))`

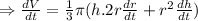
Now putting
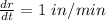`(dr)/(dt)=1 \ in/min` and
`(dh)/(dt)= -3 \ in/min`

`(dV)/(dt)=\frac13\pi \{h.2r (1)+r^2(-3)\}`

`\Rightarrow (dV)/(dt)=\frac13\pi (2hr -3r^2)`

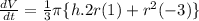
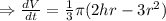
To find the rate of changing volume at the moment when base radius is 30 in and the height is 40 in, we need to put r= 30 in and h=40 in.

`(dV)/(dt)|_(r=30,h=40)=\frac13\pi \{2.40.30 -3(30)^2\}`

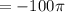`=-100\pi` cubic inches / min

The volume of the cone is shrinking at the rate
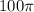`100\pi` cubic inches / min.