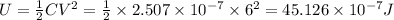Question

The parallel plates in a capacitor, with a plate area of 8.50 cm2 and an air-filled separation of 3.00 mm, are charged by a 6.00 V battery. They are then disconnected from the battery and pulled apart (without discharge) to a separation of 8.00 mm. Neglect fringing. (a) Find the potential difference between the plates. (b) Find the initial stored energy.

Answer 1

(A) Potential difference between plates will be 6 volt

(b) Initial energy stored will be
`45.126* 10^(-7)J`

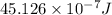
Step-by-step explanation:

It is given area of parallel late capacitor
`A=8.50cm^2=8.5* 10^(-4)m^2`

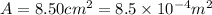
Initial voltage
`V_0=6volt`

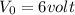
Distance between plates d = 3 mm = 0.003 m

Capacitance
`C=(\epsilon _0A)/(d)=(8.85* 10^(-7)* 8.5* 10^(-4))/(0.003)=2.507* 10^(-7)F`

So charge on the capacitor
`q_0=CV_0=2.507* 10^(-7)* 6=15.042* 10^(-7)C`

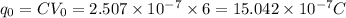
(a) This charge will be constant after disconnection.

After disconnection voltage will be

`V_1=(q_0)/(C)=(15.042* 10^(-7))/(2.507* 10^(-7))=6volt`

(b) Initial energy stored in the capacitor

`U=(1)/(2)CV^2=(1)/(2)* 2.507* 10^(-7)* 6^2=45.126* 10^(-7)J`