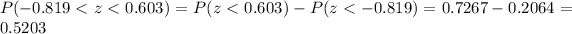Answer:
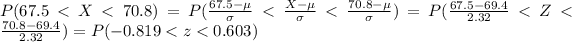
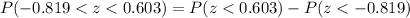
And in order to find these probabilities we can use tables for the normal standard distribution, excel or a calculator.
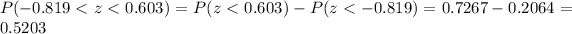
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Solution to the problem
Let X the random variable that represent the heights of a population, and for this case we know the distribution for X is given by:
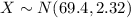
Where
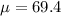 and
and
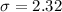
We are interested on this probability
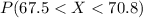
And the best way to solve this problem is using the normal standard distribution and the z score given by:
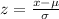
If we apply this formula to our probability we got this:
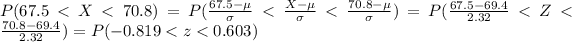
And we can find this probability with this difference:
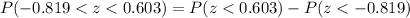
And in order to find these probabilities we can use tables for the normal standard distribution, excel or a calculator.