Answer:
The hypothesis should be retained
Explanation:
We are given:
N= 16
n = 4
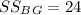
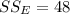
Level of significance, a = 0.05
From the given data, our ANOVA table will be:
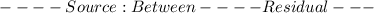
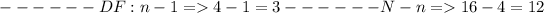
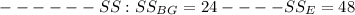
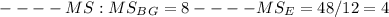
Note: proper ANOVA table is attached
The statistic will be written as:
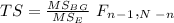
T = 8/4 = 2
Therefore
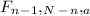
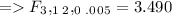
The hypothesis should be retained, because we no know that the statistic is in the acceptance area.