Answer:
95% confidence interval for the proportion of all registered voters who will vote for candidate
(0.255 ,0.344)
The lower limit of the confidence interval is 0.255
Explanation:
Explanation:-
Step1:-
Given data In a random sample of 400 registered voters, 120 indicate they plan to vote for Candidate.
n =400
The proportion of success
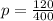
on calculation 'p' = 0.3
q =1-p
q = 1- 0.3 =0.7
Step2:-
95% confidence interval for the proportion of all registered voters who will vote for candidate
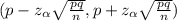
we use z- value =1.96 at 95% level of significance.
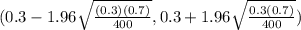
on calculation , we get
(0.3 - 0.044 ,0.3+0.044)
(0.255 ,0.344)
conclusion:-95% confidence interval for the proportion of all registered voters who will vote for candidate
(0.255 ,0.344)
The lower limit of the confidence interval is 0.255