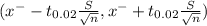Question

A botanist wishes to estimate the mean number of seeds for a certain fruit. She samples 11 specimens and finds the average number of seeds is 47 with a standard deviation of 7. Construct a 98% confidence interval for the mean number of seeds for the species using the appropriate critical value to three decimal places.

Enter your answer as equations or as numbers rounded to four decimal places.
Lower bound of CI =
Upper bound of CI =

What conditions are required for the validity of the interval?

A. μ known
B. normal population
C. random sample
D. σ known

Answer 1

a)The 98% of confidence intervals are

Lower bound of CI = 47 -3.82436 = 43.1756

Upper bound of CI = 47 + 3.82436 = 50.8243

b) The conditions are required for the validity of the interval

A) μ known

Explanation:

Explanation:-

The given sample size is 'n' =11

Given the average number of seeds is 47 with a standard deviation of 7

Sample mean (x⁻) = 47

Standard deviation (S) = 7

The 98% of confidence intervals are

`(x^(-) - t_(0.02) (S)/(√(n) ) , x^(-) + t_(0.02)(S)/(√(n) ) )`

`(47 - t_(0.02) (7)/(√(11) ) , 47+ t_(0.02)(7)/(√(11) ) )`

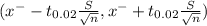
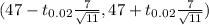
The degrees of freedom = n-1 =11-1 =10

t₀.₀₂= 1.812 ( from t - table)

now the intervals are

`(47 - 1.812 (7)/(√(11) ) , 47+ 1.812(7)/(√(11) ) )`

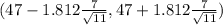
Lower bound of CI = 47 -3.82436 = 43.1756

Upper bound of CI = 47 + 3.82436 = 50.8243

The conditions are required for the validity of the interval

A) μ known

Explanation:-

If a random sample xi of size 'n' has been drawn from a normal population with a specified mean (μ) known.

The limit for (μ) is given by

`(x^(-) - t_(0.02) (S)/(√(n) ) , x^(-) + t_(0.02)(S)/(√(n) ) )`