Question

A 47.9-kg skater is standing at rest in front of a wall. By pushing against the wall she propels herself backward with a velocity of -2.34 m/s. Her hands are in contact with the wall for 1.04 s. Ignore friction and wind resistance. Find the average force she exerts on the wall (which has the same magnitude, but opposite direction, as the force that the wall applies to her). Note that this force has direction, which you should indicate with the sign of your answer.

Answer 1

The average force that the skater exerts on the wall has a value of 107.77 Newtons with opposite direction to that of the wall (with positive sign).

Step-by-step explanation:

The average force can be found employing Newton's second law:

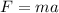`F = ma` (1)

Where F is the force, m is the mass and a is the acceleration.

The acceleration can be determined employing the equations for a Uniformly Accelerated Rectilinear Motion:

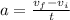`a = (v_(f)-v_(i))/(t)` (2)

Replacing equation (2) in equation (1) it is gotten:

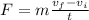`F = m(v_(f)-v_(i))/(t)` (3)

Since, the skater was standing at rest before pushing against the wall, her initial velocity will be zero (
`v_(i) = 0`)

`F = (47.9kg)((-2.34m/s)-(0m/s))/(1.04s)`

`F = -107.77kg.m/s^(2)`

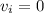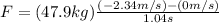
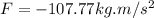
But
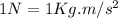`1N = 1Kg.m/s^(2)`, therefore:

`F = -107.77N`

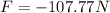
This result represents the force that the wall applies to her (as the sign shows)

According with Newton's third law, the average force that the skater exerts on the wall has a value of 107.77 Newtons with opposite direction to that of the wall (with positive sign).

Notice, that the backward direction is considered as the negative direction.