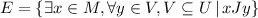Answer:
a)
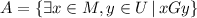 , b)
, b)
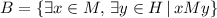 , c)
, c)
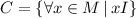 , d)
, d)
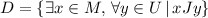 , e)
, e)
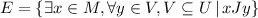
Explanation:
a) x - A student, M - Set of students of discrete math class, G - has lived in, y - Florida, U - Set of states of the United States of America.
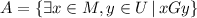
b) x - A student, M - Set of students of discrete math class, y - A perfect grade, H - Midterm I.
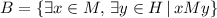
c) x - A student, M - Set of students of discrete math class, I - loves discrete math.
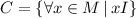
d) x - A student, M - Set of students of discrete math class, J - has been in, y - a state, U - Set of states of the United States of America.
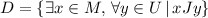
e) x - A student, M - Set of students of discrete math class, J - has been in, y - a city, V - At least one state of the United States of America, U - Set of states of the United States of America.