Answer:
99% confidence interval for the population proportion of employed individuals is [0.104 , 0.224].
Explanation:
We are given that a simple random sample of size n=250 individuals who are currently employed is asked if they work at home at least once per week.
Of the 250 employed individuals surveyed, 41 responded that they did work at home at least once per week.
Firstly, the pivotal quantity for 99% confidence interval for the population proportion is given by;
P.Q. =
 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of individuals who work at home at least once per week =
= sample proportion of individuals who work at home at least once per week =
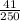 = 0.164
= 0.164
n = sample of individuals surveyed = 250
Here for constructing 99% confidence interval we have used One-sample z proportion statistics.
So, 99% confidence interval for the population proportion, p is ;
P(-2.5758 < N(0,1) < 2.5758) = 0.99 {As the critical value of z at 0.5%
level of significance are -2.5758 & 2.5758}
P(-2.5758 <
 < 2.5758) = 0.99
< 2.5758) = 0.99
P(
 <
<
 <
<
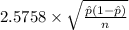 ) = 0.99
) = 0.99
P(
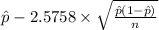 < p <
< p <
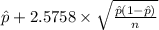 ) = 0.99
) = 0.99
99% confidence interval for p = [
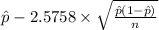 ,
,
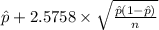 ]
]
= [
 ,
,
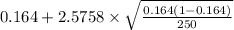 ]
]
= [0.104 , 0.224]
Therefore, 99% confidence interval for the population proportion of employed individuals who work at home at least once per week is [0.104 , 0.224].