Question

A basketball player has made 6060​% of his foul shots during the season. Assume the shots are independent. ​

a) What's the expected number of shots until he​ misses? ​
b) If the player shoots 99 foul shots in the fourth​ quarter, how many shots do you expect him to​ make? ​
c) What is the standard deviation of the 99 ​shots

Answer 1

a) 2.5 shots

b) 59.4 shots

c) 4.87 shots

Explanation:

Probability of making the shot = 0.6

Probability of missing the shot = 0.4

a) The expected number of shots until the player misses is given by:

`E(X) = (1)/(P(X))=(1)/(0.4) \\E(X) = 2.5\ shots`

The expected number of shots until the first miss is 2.5

b) The expected number of shots made in 99 attempts is:

`E=99*0.6\\E=59.4\ shots`

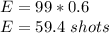
He is expected to make 59.4 shots

c) Let "p" be the proportion shots that the player make, the standard deviation for n = 99 shots is:

`s=√(n*p*(1-p))\\ s= 4.87\ shots`

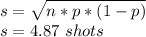
The standard deviation is 4.87 shots.