Question

A merry-go-round on a playground consists of a horizontal solid disk with a weight of 805 N and a radius of 1.47 m. A child applies a force 49.0 N tangentially to the edge of the disk to start it from rest. What is the kinetic energy of the merry-go-round disk (in J) after 2.95 s?

Answer 1

255.34 J

Step-by-step explanation:

Given,

Weight of disk = 805 N

radius = 1.47 m

Force applied by the child = 49 N

time = 2.95 s

KE = ?

mass of the disk

`M = (W)/(g)= (805)/(9.81) = 82.059\ Kg`

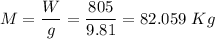
Moment of inertia of the disk

`I = (1)/(2)Mr^2`

`I = (1)/(2)* 82.059* 1.47^2 =88.66\ kgm^2`

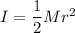
Torque on the child

`\tau = F * r = 49 * 1.47 = 72.03 Nm`

Angular acceleration

`\alpha = (\tau)/(I)=(72.03)/(88.66) = 0.812\ rad/s^2`

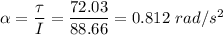
So, angular speed at t = 2.95 s

`\omega = \alpha t = 0.812 * 2.95 = 2.4\ rad/s`

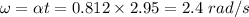
Now, KE of the merry go round

`KE = (1)/(2) I \omega^2 = (1)/(2)* 88.66* 2.4^2 = 255.34 J`

Hence, the Kinetic energy of the merry go round = 255.34 J