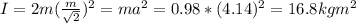Answer:
a) The rotational inertia when it passes through the midpoints of opposite sides and lies in the plane of the square is 16.8 kg m²
b) I = 50.39 kg m²
c) I = 16.8 kg m²
Step-by-step explanation:
a) Given data:
m = 0.98 kg
a = 4.14 * 4.14
The moment of inertia is:
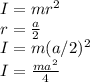
For 4 particles:
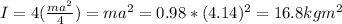
b) Distance from top left mass = x = a/2
Distance from bottom left mass = x = a/2
Distance from top right mass = x = √5 (a/2)
The total moment of inertia is:
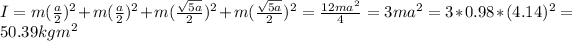
c)