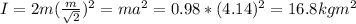Question

Four identical particles of mass 0.980 kg each are placed at the vertices of a 4.14 m x 4.14 m square and held there by four massless rods, which form the sides of the square. What is the rotational inertia of this rigid body about an axis that (a) passes through the midpoints of opposite sides and lies in the plane of the square, (b) passes through the midpoint of one of the sides and is perpendicular to the plane of the square, and (c) lies in the plane of the square and passes through two diagonally opposite particles?

Answer 1

a) The rotational inertia when it passes through the midpoints of opposite sides and lies in the plane of the square is 16.8 kg m²

b) I = 50.39 kg m²

c) I = 16.8 kg m²

Step-by-step explanation:

a) Given data:

m = 0.98 kg

a = 4.14 * 4.14

The moment of inertia is:

`I=mr^(2) \\r=(a)/(2) \\I=m(a/2)^(2) \\I=(ma^(2) )/(4)`

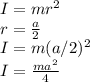
For 4 particles:

`I=4((ma^(2) )/(4) )=ma^(2) =0.98*(4.14)^(2) =16.8kgm^(2)`

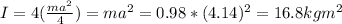
b) Distance from top left mass = x = a/2

Distance from bottom left mass = x = a/2

Distance from top right mass = x = √5 (a/2)

The total moment of inertia is:

`I=m((a)/(2) )^(2) +m((a)/(2) )^(2)+m((√(5a) )/(2) )^(2)+m((√(5a) )/(2) )^(2)=(12ma^(2) )/(4) =3ma^(2) =3*0.98*(4.14)^(2) =50.39kgm^(2)`

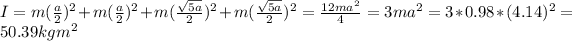
c)

`I=2m((m)/(√(2) ) )^(2) =ma^(2) =0.98*(4.14)^(2) =16.8kgm^(2)`