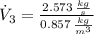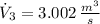Answer:
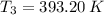 ,
,
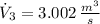
Step-by-step explanation:
This is a case of a mix chamber, which is modelled after the First Law of the Thermodynamics:
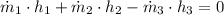
According to the Principle of Mass Conservation:

Let assume that air behaves as an ideal gas. The density has the following expression:
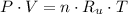
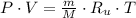
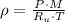
Densities at inlets are, respectively:

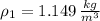


The mass flow at outlet is:
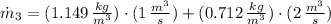

Specific enthalpies depends on temperature only. The required variable for inlet are obtained from property tables:
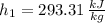
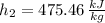
Specific enthalpy at outlet is:

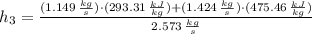
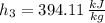
The exit temperature is:
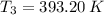
The density of air at outlet is:
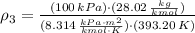

The volume flow rate at outlet is: