Question

A silicon carbide plate fractured in bending when a blunt load was applied to the plate center. The distance between the fracture origin and the mirror/mist boundary on the fracture surface was 0.796 mm. To determine the stress used to break the plate, three samples of the same material were tested and produced the following. What is the estimate of the stress present at the time of fracture for the original plate?

Mirror Radius (mm) Bending Failure Stress (MPa)
.603 225
.203 368
.162 442

Answer 1

Question in order:

A silicon carbide plate fractures in bending when a blunt load was applied to the plate center. The distance between the fracture origin and the mirror/mist boundary on the fracture surface was 0.796 mm. To determine the stress used to break the plate, three samples of the same material were tested and produced the following. What is the estimate of the stress present at the time of fracture for the original plate?

Mirror Radius (mm) Bending Failure Stress (MPa)

0.603 225

0.203 368

0.162 442

Answer:

191 MPa

Step-by-step explanation:

Failure stress of bending is Inversely proportional to the mirror radius

`Bending Stress = (1)/((Mirror Radius)^(n))`

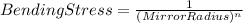
At mirror radius 1 = 0.603 mm Bending stress 1 = 225 Mpa..............(1)

At mirror radius 2 = 0.203 mm Bending stress 2 = 368 Mpa...............(2)

At mirror radius 3 = 0.162 mm Bending stress 3 = 442 Mpa...............(3)

comparing case 1 and 2 using the above equation

`(Stress 1)/(Stress 2) = ({(Radius 2)/(Radius 1)})^(n_1)`

`(225)/(368) = ({(0.203)/(0.603)})^(n_1)`

`0.6114 = (0.3366)^(n_1)`

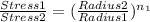
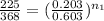
Taking the natural logarithm of both side

ln(0.6114) = n ln(0.3366)

n₁ = ln(0.6114)/ln(0.3366)

n₁ = 0.452

comparing case 2 and 3 using the above equation

`(Stress 2)/(Stress 3) = ({(Radius 3)/(Radius 2)})^(n_2)`

`(368)/(442) = ({(0.162)/(0.203)})^(n_2)`

`0.8326 = (0.7980)^(n_2)`

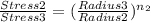
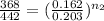
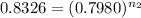
Taking the natural logarithm of both side

ln(0.8326) = n ln(0.7980)

n₂ = ln(0.8326)/ln(0.7980)

n₂ = 0.821

comparing case 1 and 3 using the above equation

`(Stress 1)/(Stress 3) = ({(Radius 3)/(Radius 1)})^(n_3)`

`(225)/(442) = ({(0.162)/(0.603)})^(n_3)`

`0.5090 = (0.2687)^(n_3)`

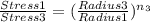
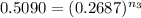
Taking the natural logarithm of both side

ln(0.5090) = n ln(0.2687)

n₃ = ln(0.5090)/ln(0.2687)

n₃ = 0.514

average for n

`n = (n_1 + n_2 + n_3)/(3)`

`n = (0.452 +0.821 + 0.514)/(3)`

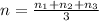
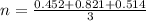
n = 0.596

Hence to get bending stress x at mirror radius 0.796

`(Stress x)/(Stress 3) = ({(Radius 3)/(Radius x)})^(0.596)`

`(Stress x)/(225) = ({(0.603)/(0.796)})^(0.596)`

`(Stress x)/(225) = 0.8475`

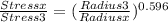
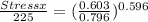
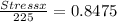
stress x = 191 MPa