Answer:
The dimension of the box are 2.878 m by 4.878 m by 0.061 m.
Explanation:
Given that,
A box is constructed from a piece of cardboard with dimensions 3 m by 5 m.
Assume the length of side of the square be x.
Then the length of the box= (3-2x) m
The width of the box is =(5-2x) meter.
The height of the box is = x m.
Then the volume of the box =length×width×height
=(3-2x)(5-2x)x cubic meters
=15x-16x²+4x³
Let,
V=15x-16x²-4x³
Differentiating with respect to x
V'= 15 - 32x+12x²
Again differentiating with respect to x
V''= -32+24x
At first we have to find out at which point the volume of the box maximum.
For that, we set V'=0
15 - 32x+12x²=0
Applying quadratic formula
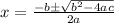 , here a= 12, b= -32 and c=15
, here a= 12, b= -32 and c=15

=2.06,0.61
So, x= 2.06 does not possible, because the length (3-2x) becomes negative.
∴x= 0.061 m
Since
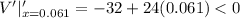 , the volume of the maximum at x =0.061 m.
, the volume of the maximum at x =0.061 m.
The length of the box is= {3- 2(0.061)} m= 2.878 m
The width of the box is ={5-2(0.061) }meter= 4.878 m
The height of the box is = 0.061 m.
The dimension of the box are 2.878 m by 4.878 m by 0.061 m.