Question

Time taken by a randomly selected applicant for a mortgage to fill out a certain form has a normal distribution with mean value 8 min and standard deviation 2 min. If five individuals fill out a form on one day and six on another, what is the probability that the sample average amount of time taken on each day is at most 11 min

Answer 1

Probability that the sample average amount of time taken on first day and second day is at most 11 min is 0.99960 and 0.99988 respectively.

Explanation:

We are given that Time taken by a randomly selected applicant for a mortgage to fill out a certain form has a normal distribution with mean value 8 min and standard deviation 2 min.

Also, five individuals fill out a form on one day and six on another.

Let
`\bar X` = sample average amount of time taken on each day

The z-score probability distribution for sample mean is given by;

Z =
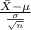`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = mean time taken = 8 min

`\sigma` = standard deviation = 2 min

n = sample of individuals = 5 on first day and 6 on another day

(a) Probability that the sample average amount of time taken on first day by five individuals is at most 11 min is given by;

P(
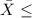`\bar X \leq` 11 min) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )`
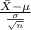
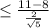`\leq (11-8)/((2)/(√(5) ) )` ) = P(Z
`\leq` 3.35) = 0.99960

The above probability is calculated by looking at the value of x = 3.35 in the z table which gave an area of 0.99960.

(b) Probability that the sample average amount of time taken on another day by six individuals is at most 11 min is given by;

P(
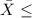`\bar X \leq` 11 min) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )`
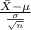
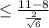`\leq (11-8)/((2)/(√(6) ) )` ) = P(Z
`\leq` 3.67) = 0.99988

The above probability is calculated by looking at the value of x = 3.67 in the z table which gave an area of 0.99988.

Therefore, the probability that the sample average amount of time taken on first day and second day is at most 11 min is 0.99960 and 0.99988 respectively.