Question

Scores on a certain test are normally distributed with a variance of 14. A researcher wishes to estimate the mean score achieved by all adults on the test. Find the sample size needed to assure with 98% confidence that the sample mean will not differ from the population mean by more than 2 units.

Answer 1

The sample size must be 20 so that sample mean will not differ from the population mean by more than 2 units.

Explanation:

We are given the following in the question:

Variance = 14

`\sigma^2 = 14\\\sigma = √(14)`

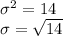
We need to form a 9% confidence interval such that sample mean will not differ from the population mean by more than 2 units.

Thus, margin of error for the confidence interval is 2.

Formula for margin of error:

`z_(critical)* (\sigma)/(√(n))`

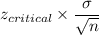
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.05) = 2.33`

`2 = 2.33* (√(14))/(√(n))\\\\√(n) = (2.33* √(14))/(2)\\\\√(n)=4.359\\\Rightarrow n = 19.00115\approx 20`

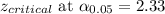
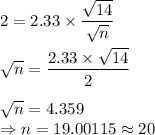
Thus, the sample size must be 20 so that sample mean will not differ from the population mean by more than 2 units.