Answer:
Explanation:
Hello!
The objective is to test if the courses emphasize memorizing facts, ideas or methods following the same distribution as before.
The variable of interest is
X: Opinion of students in how much of their coursework emphasized memorizing facts, ideas, or methods. Categorized: 1_"Very little", 2_" Some", 3_" Quite a bit" and 4_"Very much"
It is known for a survey made in 2014 that the percentages for each category are: 1_Very little: 21.5%, 2_Some: 33.7%, 3_Quite a bit: 27.7% and 4_Very much: 17.1%
To test if the current situation follows the same distribution as the historical data (from 2014) you have to conduct a Goodness to Fit Chi-Square test.
The hypotheses are:
H₀: P₁= 0.215; P₂= 0.337, P₃= 0.277 and P₄= 0.171
H₁:
α: 0.01
![X^2= sum[((O:i-E_i)^2)/(E_i) ]~~X^2_(k-1)](https://img.qammunity.org/2021/formulas/mathematics/college/imp18umkvapfdosb1dort44zh1a6k3vsy6.png)
k= number of categories of the variable.
This test is always one-tailed (right), which means that you will reject the null hypothesis to high values of X² (when the observed and expected frequencies for each category are too different)
The critical value is:
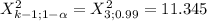
You will reject the null hypothesis if
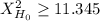
You will not reject the null hypothesis if
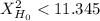
Before calculating the statistic under the null hypothesis, you have to calculate the expected value for each category following the formula:
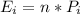
n= 400
E₁= n*P₁= 400*0.215= 86
E₂= n*P₂= 400*0.337= 134.8
E₃= n*P₃= 400*0.277= 110.8
E₄=n*P₄= 400*0.171= 68.4
The observed frequencies are:
O₁= 39
O₂= 139
O₃= 148
O₄= 74
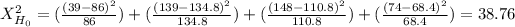
As said before, this test is one-tailed to the right (always) and so is its p-value:
P(X₃²≥38.76)= 1 - P(X²₃<38.76)= 1 - 1 ≅ 0
p-value < 0.00001
Using both approaches (p-value and critical value) the decision is to reject the null hypothesis.
With a level of significance of 1% the decision is to reject the null hypothesis, then the actual courses do not emphasize the memorization of facts, ideas, and methods following the historical percentages.
I hope this helps!