Answer:
As slit separation (
 ) is increased, angle of first diffraction minimum will remains same.
) is increased, angle of first diffraction minimum will remains same.
As slit separation (
 ) is increased, angle to the first interference maximum is decrease
) is increased, angle to the first interference maximum is decrease
Step-by-step explanation:
Given:
From the formula of interference and diffraction,
⇒ For diffraction,
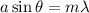
Where
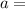 width of slit,
width of slit,
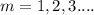
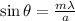
⇒ For interference,
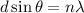
Where
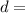 distance between two slit,
distance between two slit,

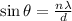
As slit separation (
 ) is increased, angle of first diffraction minimum will remains same.
) is increased, angle of first diffraction minimum will remains same.
As slit separation (
 ) is increased, angle to the first interference maximum is decrease
) is increased, angle to the first interference maximum is decrease