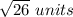Rectangle WXYZ is shown on a coordinate plane. What is the length of side XY?

Question

asked Jun 21, 2021 204k views

2 Answers

Rtn · Answer 1 · 2021-06-27T11:16:33+0000

Answer:

The length of side XY is
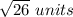
$√(26)\ units$

Explanation:

The picture of the question in the attached figure

we know that

the formula to calculate the distance between two points is equal to

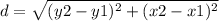
$d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}$

we have that the coordinates of points X and Y are

X(4,2) and Y(3,-3)

substitute the given values in the formula

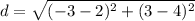
$d=\sqrt{(-3-2)^(2)+(3-4)^(2)}$

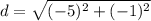
$d=\sqrt{(-5)^(2)+(-1)^(2)}$

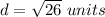
$d=√(26)\ units$

therefore

The length of side XY is
$√(26)\ units$