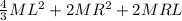Answer:
I=
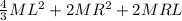
Step-by-step explanation:
We are given that
Mass of rod=M
Length of rod=L
Mass of hoop=M
Radius of hoop=R
We have to find the moment of inertia I of the pendulum about pivot depicted at the left end of the slid rod.
Moment of inertia of rod about center of mass=
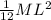
Moment of inertia of hoop about center of mass=
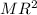
Moment of inertia of the pendulum about the pivot left end,I=

Moment of inertia of the pendulum about the pivot left end,I=

Moment of inertia of the pendulum about the pivot left end,I=
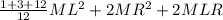
Moment of inertia of the pendulum about the pivot left end,I=
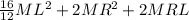
Moment of inertia of the pendulum about the pivot left end,I=