Answer:
a) The work done is 160.52 J
b) The change in the gravitational potential energy on the snowball is -160.52 J
c) The gravitational potential energy that is taken to be zero at the height of the cliff is -160.52 J
Step-by-step explanation:
Given:
m = 1.8 kg
h = 9.1 m
vi = 17.4 m/s
θ = 44°
a) The work done on the snowball is:
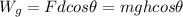
Here θ = 0 because they are in the same direction
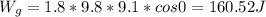
b) The change in the gravitational potential energy on the snowball is:
ΔU = -Wg = -160.52 J
c) The gravitational potential energy that is taken is:
