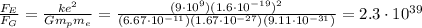Question

Is it possible to have a charge of 5 x 10-20 C? Why?

Is it possible to have a charge of 2.4 x 10--18 C? Why?
Is it possible to have a charge of 2.0 x 10-19 C? Why?
Two charges Q and 5Q, are separated by some distance. How do the forces compare on each charge? Why?
What is the electric force between charges of +4.5 x 10-6 C and +7.2 x 10-6 C when they are separated by a distance of 0.30 cm? Is it attractive or repulsive?
A hydrogen atom is made up of 1 proton and 1 electron separated by a distance of 5.3x10−11m. How does the electric force compare to the gravitational force between these particles?

Answer 1

1) No

2) Yes

3) No

4) Equal and opposite

5) 32400 N

6) Repulsive

7) The electric force is
`2.3\cdot 10^(39)` times bigger than the gravitational force

Step-by-step explanation:

1)

In nature, the minimum possible charge that an object can have is the charge of the electron, which is called fundamental charge:

`e=1.6\cdot 10^(-19)C`

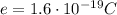
Electrons are indivisible particles (they cannot be separated), this means that an object can have at least the charge equal to the charge of one electron (in fact, it cannot have a charge less than
`e`, because it would meant that the object has a "fractional number" of electrons).

In this problem, the object has a charge of

`Q=5\cdot 10^(-20)C`

If we compare this value to
`e`, we notice that
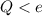`Q<e`, so no object can have a charge of
`Q`.

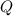2)

As we said in part 1), an object should have an integer number of electrons in order to be charged.

This means that the charge of an object must be an integer multiple of the fundamental charge, so we can write it as:

`Q=ne`

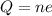
where

Q is the charge of the object

n is an integer multiple

e is the fundamental charge

Here we have

`Q=2.4\cdot 10^(-18)C`

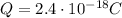
Substituting the value of e, we find n:

`n=(Q)/(e)=(2.4\cdot 10^(-18))/(1.6\cdot 10^(-19))=15`

n is integer, so this value of the charge is possible.

3)

We now do the same procedure for the new object in this part, which has a charge of

`Q=2.0\cdot 10^(-19)C`

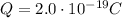
Again, the charge on this object can be written as

`Q=ne`

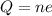
where

n is the number of electrons in the object

Using the value of the fundamental charge,

`e=1.6\cdot 10^(-19)C`

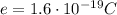
We find:

`n=(Q)/(e)=(2.0\cdot 10^(-19))/(1.6\cdot 10^(-19))=1.25`

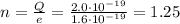
n is not integer, so this value of charge is not possible, since an object cannot have a fractional number of electrons.

4)

To solve this part, we use Newton's third law of motion, which states that:

"When an object A exerts a force on an object B (Action force), then object B exerts an equal and opposite force on object A (reaction force)".

In this problem, we have two objects:

- A charge Q

- A charge 5Q

Charge Q exerts an electric force on charge 5Q, and we can call this action force. At the same time, charge 5Q exerts an electric force on charge Q (reaction force), and according to Newton's 3rd law, the two forces are equal and opposite.

5)

The magnitude of the electric force between two single-point charges is

`F=k(q_1 q_2)/(r^2)`

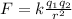
where

k is the Coulomb's constant

q1, q2 are the two charges

r is the separation between the two charges

In this problem we have:

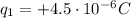`q_1=+4.5\cdot 10^(-6)C` is charge 1

`q_2=+7.2\cdot 10^(-6)C` is charge 2

r = 0.30 cm = 0.003 m is the separation

So, the electric force between the two charges is

`F=(9\cdot 10^9)((4.5\cdot 10^(-6))(7.2\cdot 10^(-6)))/((0.003)^2)=32400 N`

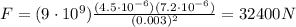
6)

The electric force between two charged objects has direction as follows:

- If the two objects have charges of opposite signs (+ and -), the force between them is attractive

- If the two objects have charges of same sign (++ or --), the force between them is repulsive

In this problem, the two charges are:

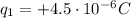`q_1=+4.5\cdot 10^(-6)C` is charge 1

`q_2=+7.2\cdot 10^(-6)C` is charge 2

We see that the two charges have same sign: therefore, the force between them is repulsive.

7)

The electric force between the proton and the electron in the atom can be written as

`F_E=k(q_1 q_2)/(r^2)`

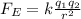
where

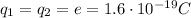`q_1 = q_2 = e = 1.6\cdot 10^(-19)C` is the magnitude of the charge of the proton and of the electron

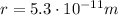`r=5.3\cdot 10^(-11) m` is the separation between them

So the force can be rewritten as

`F_E=(ke^2)/(r^2)`

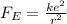
The gravitational force between the proton and the electron can be written as

`F_G=G(m_p m_e)/(r^2)`

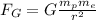
where

G is the gravitational constant

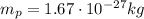`m_p = 1.67\cdot 10^(-27)kg` is the proton mass

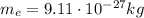`m_e=9.11\cdot 10^(-27)kg` is the electron mass

Comparing the 2 forces,

`(F_E)/(F_G)=(ke^2)/(Gm_p m_e)=((9\cdot 10^9)(1.6\cdot 10^(-19))^2)/((6.67\cdot 10^(-11))(1.67\cdot 10^(-27))(9.11\cdot 10^(-31)))=2.3\cdot 10^(39)`