Question

For a certain​ automobile,

Upper M left parenthesis x right parenthesis equals negative . 015 x squared plus 1.21 x minus 7.8M(x)=−.015x2+1.21x−7.8​,

30 less than or equals x less than or equals 6030≤x≤60​,

represents the miles per gallon obtained at a speed of x miles per hour.

​(a) Find the absolute maximum miles per gallon and the speed at which it occurs.

​(b) Find the absolute minimum miles per gallon and the speed at which it occurs.

Answer 1

(a)Max M=16.6, at x=40.33 miles per hour.

(b)Minimum M=10.8 at x=60 miles per hour.

Explanation:

The function which represents the miles per gallon obtained at a speed of x miles per hour is given as:

`M(x)=-0.015x^2+1.21x-7.8`, 30≤x≤60

To obtain the absolute maximum and minimum miles per gallon, we find the derivative of M(x), set it equal to zero and solve for the critical points.

`M^(')(x)=-0.03x+1.21=0\\-0.03x=-1.21\\x=40.33`

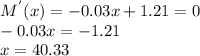
Next, we evaluate the function at the end-points and the critical point.

`M(30)=-0.015(30)^2+1.21(30)-7.8=15\\M(40.33)=-0.015(40.33)^2+1.21(40.33)-7.8=16.6\\M(60)=-0.015(60)^2+1.21(60)-7.8=10.8`

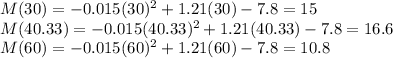
(a)Thus, the maximum absolute miles per gallon is 16.6 which occurs at a speed of x=40.33 miles per hour.

(b)The minimum absolute miles per gallon is 10.8 which occurs at a speed of x=60 miles per hour.