Question

The function f (x )equals x cubed minus 2 is​ one-to-one. Find an equation for f Superscript negative 1 Baseline (x )​, the inverse function. f Superscript negative 1 Baseline (x )equals nothing

Answer 1

a

Explanation:

Answer 2

Inverse of given function
`f\left(x\right)=x^(3)-2` is
`f^(-1)\left(x\right)=\sqrt[3]{x+2}`

Explanation:

Given that
`f\left(x\right)=x^(3)-2` and it is one to one function.

Following are the steps to find the inverse of the above function.

Step 1: Replace
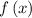`f\left(x\right)` with y

`y=x^(3)-2`

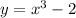
Step 2: Interchange x and y.

`x=y^(3)-2`

Step 3: Solve for y.

Rewriting the equation in step 2,

`y^(3)-2=x`

Add 2 on both sides,

`y^(3)-2+2=x+2`

`y^(3)=x+2`

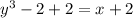
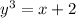
Taking cube root on both sides,

`\sqrt[3]{y^(3)}=\sqrt[3]{x+2}`

Applying radical rule,

`\sqrt[n]{x^(m)}=x^{(m)/(n)}`

So,

`\left(y^(3)\right)^{(1)/(3)}=\sqrt[3]{x+2}`

Simplifying,

`y=\sqrt[3]{x+2}`

The resulting equation is inverse function of the given function.

`\therefore f^(-1)\left(x\right)=\sqrt[3]{x+2}`