Answer:
Explanation:
Hello!
You have the data of two The National Health Interview Survey conducted in 1991 and 2003 by the U.S. National Center for Health Statistics.
Let
X₁: The number of adults that were smokers in 1991
n₁= 42000
p'₁= 0.256
X₂: The number of adults that were smokers in 2003
n₂= 33326
p'₂= 0.214
The parameter of interest is the difference between the population proportion of adult smokers in 1991 and the population proportion of adult smokers in 2003, symbolically: "p₁ - p₂"
a) The point estimate of "p₁ - p₂" ios the difference between the sample proportions:
p'₁ - p'₂= 0.256-0.214= 0.042
b) and c)
To estimate the difference of proportions using a CI, you have to apply the central limit theorem and approximate the distribution of the sample proportions to normal. for this approximation to be valid, the sample size for both populations should be high enough (n≥30) and the populations should be at least 20 times bigger than the sample taken. Both samples should be random and independent. Each sample must have at least 10 successes and at least 10 failures. If all conditions are met you can calculate the 99% CI as:
(p'₁-p'₂)±
 *
*
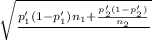
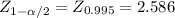
(0.042) ± 2.586*
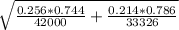
[0.034; 0.050]
Using a 99% confidence level you'd expect that the interval [0.034; 0.050] will include the true value of the difference between the proportion of adult smokers in 1991 and the proportion of adult smokers in 2003.
I hope this helps!