Answer:
The mean of the distribution of sample means is 27.6
Explanation:
We are given the following in the question:
Mean, μ = 27.6
Standard Deviation, σ = 39.4
We are given that the population is a bell shaped distribution that is a normal distribution.
Sample size, n = 173.
We have to find the mean of the distribution of sample means.
Central Limit theorem:
- It states that the distribution of the sample means approximate the normal distribution as the sample size increases.
- The mean of all samples from the same population will be approximately equal to the mean of the population.
Thus, we can write:
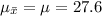
Thus, the mean of the distribution of sample means is 27.6